Inverse scattering for wafer metrology

Nowadays, society depends on electronic devices for work, transportation, communication, entertainment, and more. To further improve these devices in terms of a reduced power consumption or increased memory capacity, the core of these devices in the form of integrated circuits (ICs) need to be produced with even smaller structures and finer details. A crucial part within the fabrication process of ICs is accurate monitoring such that production defects can be detected and calibration of the fabrication process can be performed to mitigate these production effects for the next batch of ICs. Failure to do so may result in the production of faulty ICs. We developed computational techniques that are capable of accurately estimating the shape and material properties of these structures, representing the particular details of an IC, during the fabrication process. 

Inverse scattering for wafer metrology focuses on retrieving the geometrical and material properties of structures by analyzing their electromagnetic response. Inversion plays a key role in wafer metrology in which parts of the structures on a wafer are monitored as a means to detect possible production errors.

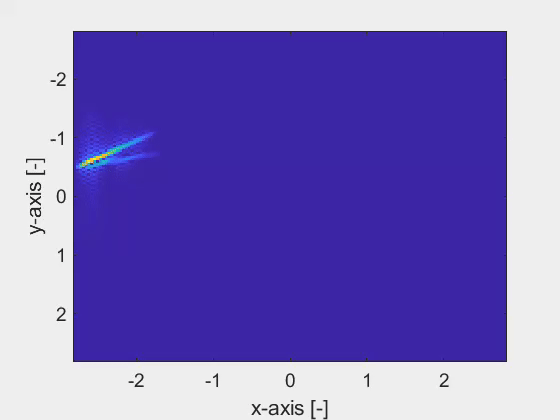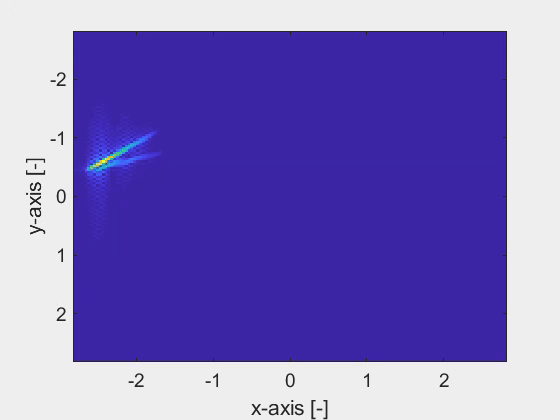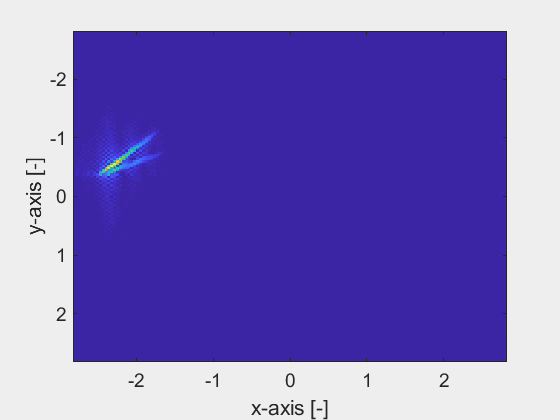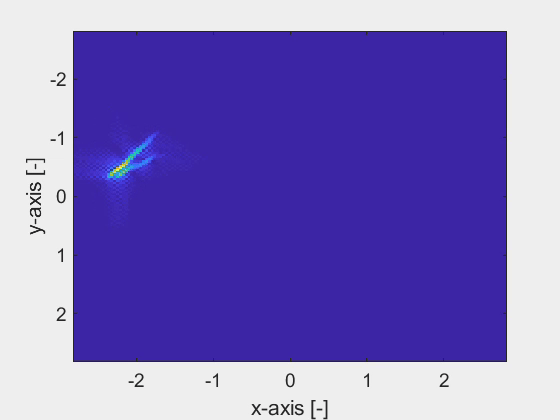
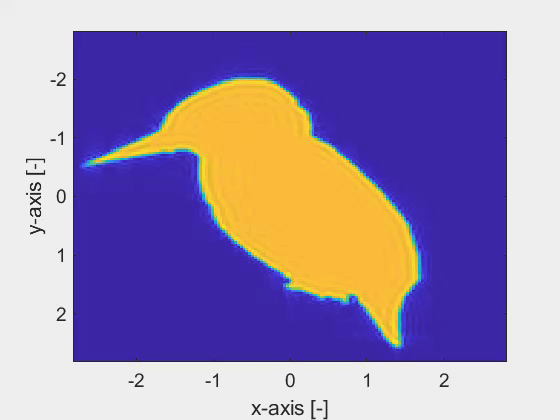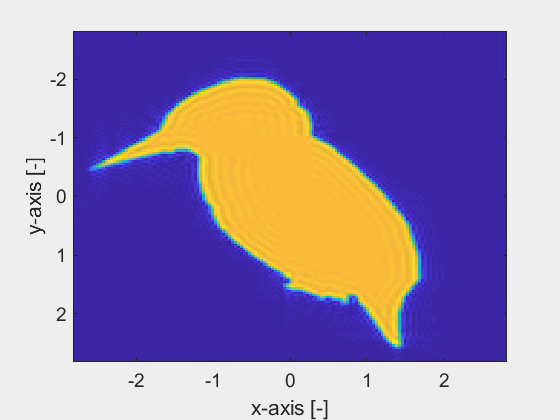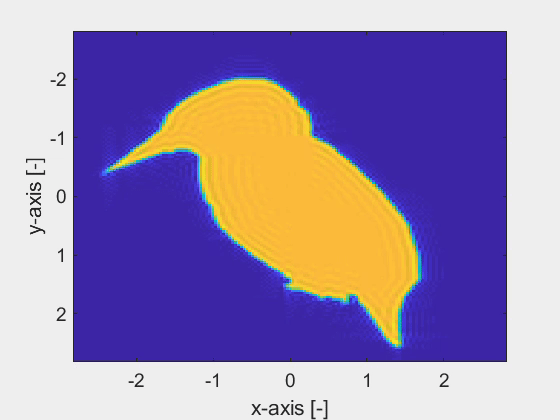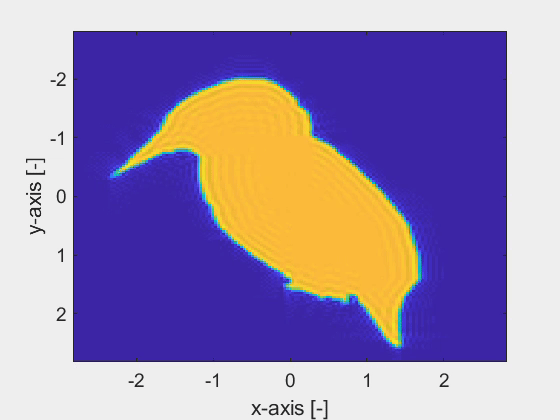
We have developed a noise-robust electromagnetic inversion algorithm, based on the spatial spectral Maxwell solver, to accurately retrieve the geometrical and material properties of finite three-dimensional dielectric objects in a planarly layered background medium. The spatial spectral Maxwell solver employs a Gabor-frame expansion, which yields a meshless definition of the objects. In other words, the resolution of retrieving the fine geometrical details of an object is not tied to a grid. An example of a Gabor-frame expanded object is shown in the first figure, which shows the top-view of an object with its cross-section shaped as a kingfisher. The second figure shows the analytic derivative with respect to the tip of the kingfisher鈥檚 beak, acting as a parameter. This derivative is readily obtained owing to the Gabor-frame expansion in the spatial spectral Maxwell solver. 

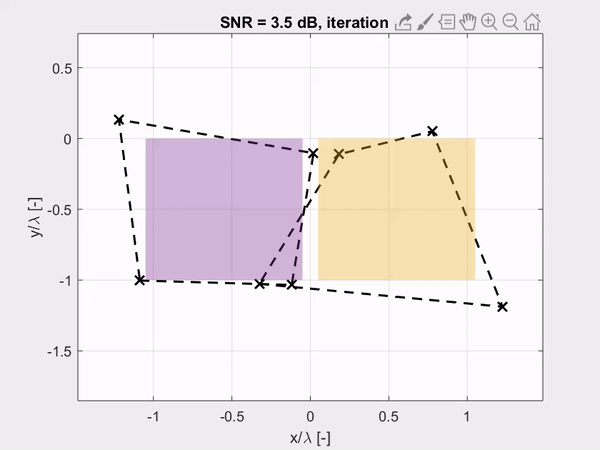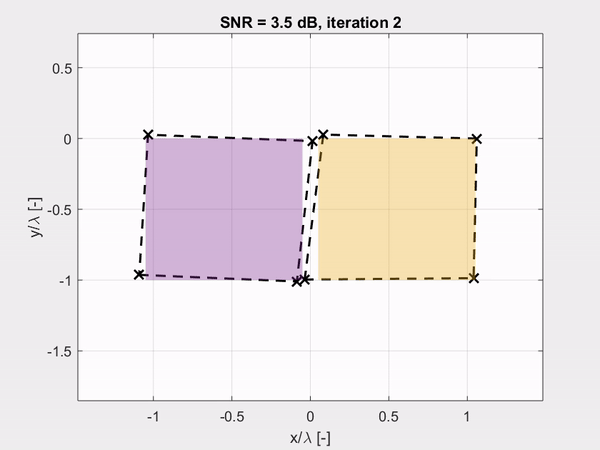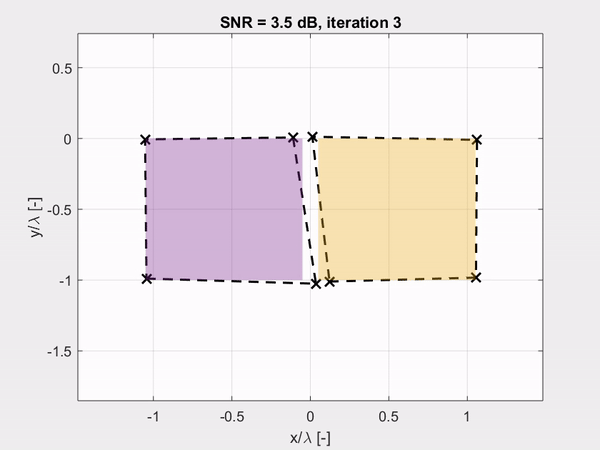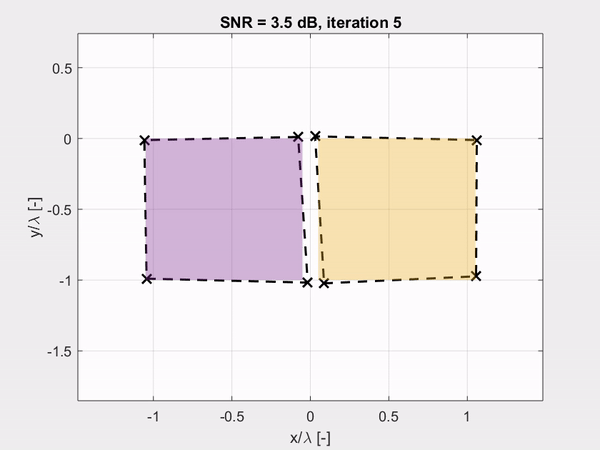
The combination of the spatial spectral Maxwell solver and the derivatives of the parametrized objects leads to a noise-robust estimation of the fine geometrical details of an object as shown by the last animation. Here, the corner points of the cross-section of the objects are accurately retrieved with nanometer precision within only a few iterations of the inversion algorithm, despite the high-noise levels.